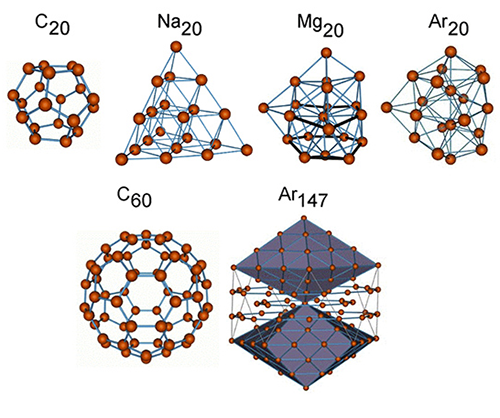
A group of atoms bound together by interatomic forces is called an atomic cluster. In nature, there are many different types of atomic clusters: van der Waals clusters, metallic clusters, fullerenes, molecular, semiconductor, mixed clusters, and their shapes can depart considerably from the common spherical form: arborescent, linear, spirals, etc. Usually, one can distinguish between different types of clusters by the nature of the forces between the atoms or by the principles of spatial organization within the clusters. There is no qualitative distinction between small clusters and molecules; however, as the number of atoms in the system increases, atomic clusters acquire more and more specific properties, making them unique physical objects different from both single molecules and from the solid state.
The novelty of atomic cluster physics arises mainly from the fact that cluster properties explain the transition from single atoms or molecules to the solid state. We employ modern theoretical approaches to study this transition. We are particularly interested in exploring the mechanisms of cluster growth and the manifestation of various collective properties, such as plasmon excitations, electron conduction band formation, superconductivity and superfluidity, phase transitions, fission and many more.
