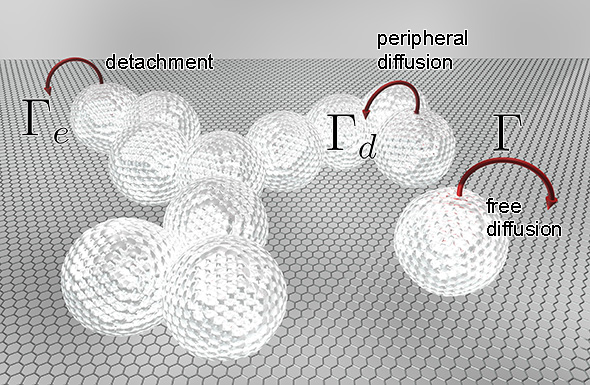
The overarching goal of nanotechnology is to create nanostructured materials that are not only controllable but also reproducible on an industrial scale. Achieving this level of precision in material design hinges on our ability to fine-tune critical parameters that dictate their final architecture. In pursuit of this ambitious aim, this research project centers on the fascinating world of dendritic structures, more commonly known as fractals, and their formation on surfaces. What makes this endeavor particularly captivating is that fractals emerge in environments far from equilibrium, challenging our understanding of growth dynamics. To delve into the intricate world of self-organization and stability within these fractals, we employ cutting-edge stochastic dynamics techniques developed within our research group. Our focus lies in unraveling the post-growth processes within these fractal structures. Our theoretical approach goes beyond the surface and accounts for a myriad of dynamic phenomena taking place within the system. We're keenly interested in modelling how particles within a fractal interact, diffuse, and detach, as these intricate processes hold the key to shaping the ultimate form of the nanostructures on the surface. Moreover, we pay meticulous attention to the interparticle interactions and diffusion barriers governing various kinetic processes. This research is not just a theoretical exercise; it holds immense practical significance for nanotechnology. By gaining a profound understanding of these intricate dynamics, we provide invaluable insights into the controlled design of nanostructured materials, paving the way for innovative applications and breakthroughs in this exciting frontier of science.
